# Install and load libraries.
library(xlsx)
## Loading required package: rJava
## Loading required package: xlsxjars
library(ggplot2)
library(car)
## Warning: package 'car' was built under R version 3.4.4
## Loading required package: carData
## Warning: package 'carData' was built under R version 3.4.4
# Question 1
# Import the data from the Excel file containing data in Assignment 4.
occupation.prestige <- read.xlsx("homework4data.xlsx", sheetName = "Sheet1", header = TRUE)
colnames(occupation.prestige) <- c("Title", "Education", "Income", "Percent_of_Women", "Prestige_Score")
head(occupation.prestige) ; tail(occupation.prestige)
## Title Education Income Percent_of_Women Prestige_Score
## 1 GOV_ADMINISTRATORS 13.11 12351 11.16 68.8
## 2 GENERAL_MANAGERS 12.26 25879 4.02 69.1
## 3 ACCOUNTANTS 12.77 9271 15.70 63.4
## 4 PURCHASING_OFFICERS 11.42 8865 9.11 56.8
## 5 CHEMISTS 14.62 8403 11.68 73.5
## 6 PHYSICISTS 15.64 11030 5.13 77.6
## Title Education Income Percent_of_Women Prestige_Score
## 97 TRAIN_ENGINEERS 8.49 8845 0.00 48.9
## 98 BUS_DRIVERS 7.58 5562 9.47 35.9
## 99 TAXI_DRIVERS 7.93 4224 3.59 25.1
## 100 LONGSHOREMEN 8.37 4753 0.00 26.1
## 101 TYPESETTERS 10.00 6462 13.58 42.2
## 102 BOOKBINDERS 8.55 3617 70.87 35.2
# Question 2
# Generate scatterplot for Prestige_Score and Education
png("scatterPlot.png", width = 1000, height = 750, unit = "px") # Export plot as PNG file
plot(occupation.prestige$Education, occupation.prestige$Prestige_Score,
main = "Scatter Plot of Education Level vs. Prestige Score",
xlab = "Education Level (years)", ylab = "Prestige Score",
type = "n", xlim = c(min(occupation.prestige$Education), max(occupation.prestige$Education)),
ylim = c(min(occupation.prestige$Prestige_Score), max(occupation.prestige$Prestige_Score)))
plot(occupation.prestige$Education, occupation.prestige$Prestige_Score,
main = "Scatter Plot of Education Level vs. Prestige Score",
xlab = "Education Level (years)", ylab = "Prestige Score",
type = "n")
grid()
points(occupation.prestige$Education, occupation.prestige$Prestige_Score, col = "steelblue", pch = 20)
dev.off()
## quartz_off_screen
## 2
# Calculate the correlation.
cor(occupation.prestige$Education, occupation.prestige$Prestige_Score)
## [1] 0.8501769
# Question 3
# Perform a simple linear regression.
m <- lm(Prestige_Score ~ Education, data = occupation.prestige) ; m
##
## Call:
## lm(formula = Prestige_Score ~ Education, data = occupation.prestige)
##
## Coefficients:
## (Intercept) Education
## -10.732 5.361
# Generate and save the residual plot.
png("residualPlot.png", width = 1000, height = 750, unit = "px") # Export plot as PNG file
plot(m, which = 1, col = "steelblue", pch = 20)
dev.off()
## quartz_off_screen
## 2
# Generate a histogram of the residuals.
png("residualPlotHist.png", width = 1000, height = 750, unit = "px") # Export plot as PNG file
hist(residuals(m), main = "Histogram of the Residuals for Prestige Score ~ Education", col = "steelblue")
dev.off()
## quartz_off_screen
## 2
# Identify outliers by ID (Title).
outlierTest(m)
## No Studentized residuals with Bonferonni p < 0.05
## Largest |rstudent|:
## rstudent unadjusted p-value Bonferonni p
## 53 -2.98896 0.0035306 0.36012
influence.measures(m)
## Influence measures of
## lm(formula = Prestige_Score ~ Education, data = occupation.prestige) :
##
## dfb.1_ dfb.Edct dffit cov.r cook.d hat inf
## 1 -0.061640 0.089475 0.13600 1.017 9.24e-03 0.01729
## 2 -0.046715 0.087777 0.17951 0.984 1.59e-02 0.01288
## 3 -0.030017 0.046759 0.07804 1.028 3.06e-03 0.01530
## 4 0.000112 0.017378 0.07133 1.021 2.56e-03 0.01042
## 5 -0.074698 0.093601 0.11422 1.043 6.56e-03 0.02985
## 6 -0.076393 0.091628 0.10474 1.059 5.53e-03 0.04176
## 7 -0.035776 0.043812 0.05164 1.056 1.35e-03 0.03499
## 8 -0.098101 0.118487 0.13682 1.052 9.41e-03 0.03921
## 9 -0.073971 0.093220 0.11475 1.041 6.62e-03 0.02883
## 10 -0.013436 0.016818 0.02049 1.052 2.12e-04 0.03005
## 11 -0.023925 0.042224 0.08123 1.024 3.32e-03 0.01343
## 12 -0.016454 0.030280 0.06072 1.028 1.86e-03 0.01305
## 13 0.091907 -0.121853 -0.16216 1.020 1.31e-02 0.02252
## 14 0.053768 -0.068085 -0.08443 1.045 3.59e-03 0.02803
## 15 -0.101343 0.128978 0.16119 1.030 1.30e-02 0.02725
## 16 0.115088 -0.147966 -0.18784 1.020 1.76e-02 0.02584
## 17 -0.149751 0.178865 0.20324 1.047 2.07e-02 0.04348
## 18 0.076137 -0.098313 -0.12564 1.034 7.92e-03 0.02529
## 19 0.193132 -0.235241 -0.27504 1.018 3.74e-02 0.03652
## 20 -0.071104 0.089712 0.11064 1.042 6.16e-03 0.02863
## 21 -0.180068 0.213785 0.24086 1.044 2.89e-02 0.04621
## 22 0.023260 -0.031494 -0.04327 1.040 9.45e-04 0.02085
## 23 0.058754 -0.071984 -0.08490 1.053 3.63e-03 0.03488
## 24 -0.229559 0.272622 0.30727 1.029 4.68e-02 0.04607
## 25 0.147272 -0.175000 -0.19740 1.052 1.95e-02 0.04579
## 26 -0.003582 0.004467 0.00541 1.053 1.48e-05 0.03079
## 27 -0.035198 0.060375 0.11272 1.016 6.36e-03 0.01375
## 28 -0.038895 0.026171 -0.06106 1.026 1.88e-03 0.01201
## 29 -0.085572 0.115864 0.15918 1.017 1.26e-02 0.02085
## 30 0.022881 -0.027881 -0.03262 1.058 5.37e-04 0.03640
## 31 -0.052105 0.080764 0.13395 1.013 8.96e-03 0.01540
## 32 0.011121 0.012069 0.09388 1.013 4.41e-03 0.00997
## 33 -0.000985 0.001558 0.00265 1.036 3.55e-06 0.01498
## 34 -0.000212 0.009914 0.03961 1.028 7.91e-04 0.01046
## 35 0.003498 -0.018573 -0.06203 1.024 1.94e-03 0.01077
## 36 0.002304 -0.027291 -0.10224 1.011 5.23e-03 0.01056
## 37 -0.000226 -0.001296 -0.00619 1.031 1.93e-05 0.01025
## 38 -0.012283 0.001583 -0.04387 1.026 9.70e-04 0.00982
## 39 -0.000622 -0.006184 -0.02769 1.029 3.87e-04 0.01032
## 40 -0.066681 0.047837 -0.09565 1.020 4.59e-03 0.01307
## 41 0.057290 -0.120050 -0.26932 0.921 3.46e-02 0.01223 *
## 42 -0.014722 -0.011925 -0.10788 1.007 5.81e-03 0.00993
## 43 -0.022408 0.015915 -0.03261 1.032 5.37e-04 0.01287
## 44 -0.032084 0.016321 -0.06831 1.022 2.35e-03 0.01040
## 45 -0.026901 0.006919 -0.08267 1.016 3.43e-03 0.00987
## 46 -0.017888 -0.037964 -0.22633 0.933 2.46e-02 0.01009 *
## 47 0.002490 0.003418 0.02392 1.029 2.89e-04 0.01001
## 48 0.000322 -0.041939 -0.16981 0.976 1.42e-02 0.01044
## 49 -0.021146 -0.013460 -0.14015 0.991 9.73e-03 0.00990
## 50 -0.003213 0.001878 -0.00598 1.031 1.81e-05 0.01088
## 51 -0.010089 -0.013849 -0.09693 1.012 4.70e-03 0.01001
## 52 -0.090894 0.046930 -0.19104 0.963 1.78e-02 0.01043
## 53 -0.191802 0.122576 -0.32191 0.868 4.80e-02 0.01147 *
## 54 -0.114703 0.063968 -0.22425 0.941 2.43e-02 0.01067
## 55 0.002851 -0.014444 -0.04773 1.027 1.15e-03 0.01079
## 56 -0.002116 -0.002296 -0.01786 1.030 1.61e-04 0.00997
## 57 0.004162 0.003177 0.02971 1.029 4.45e-04 0.00992
## 58 0.026503 -0.017736 0.04191 1.030 8.86e-04 0.01194
## 59 0.007220 0.002891 0.04099 1.027 8.47e-04 0.00985
## 60 -0.015447 0.012965 -0.01749 1.043 1.54e-04 0.02176
## 61 -0.170428 0.134528 -0.21150 0.984 2.20e-02 0.01647
## 62 0.030055 -0.006096 0.09869 1.010 4.87e-03 0.00984
## 63 -0.109537 0.073503 -0.17258 0.983 1.47e-02 0.01198
## 64 -0.126493 0.108599 -0.13885 1.031 9.66e-03 0.02525
## 65 -0.173952 0.150877 -0.18845 1.023 1.77e-02 0.02731
## 66 -0.149981 0.127078 -0.16758 1.020 1.40e-02 0.02307
## 67 0.338779 -0.297116 0.36208 0.967 6.35e-02 0.03001
## 68 -0.155702 0.121569 -0.19650 0.988 1.90e-02 0.01588
## 69 -0.015692 0.011819 -0.02093 1.035 2.21e-04 0.01440
## 70 0.142332 -0.120867 0.15855 1.023 1.26e-02 0.02341
## 71 -0.075307 0.063587 -0.08455 1.037 3.60e-03 0.02257
## 72 0.068541 -0.057874 0.07695 1.038 2.98e-03 0.02257
## 73 -0.092928 0.079420 -0.10262 1.037 5.30e-03 0.02445
## 74 0.154960 -0.136661 0.16455 1.036 1.36e-02 0.03160
## 75 0.063563 -0.055956 0.06764 1.050 2.31e-03 0.03106
## 76 -0.004478 0.002243 -0.00966 1.031 4.71e-05 0.01036
## 77 0.079278 -0.060303 0.10415 1.021 5.44e-03 0.01475
## 78 0.019036 -0.015178 0.02326 1.037 2.73e-04 0.01707
## 79 0.140145 -0.116239 0.16141 1.016 1.30e-02 0.02037
## 80 0.016950 -0.013475 0.02081 1.037 2.19e-04 0.01689
## 81 0.076645 -0.058535 0.10007 1.022 5.02e-03 0.01490
## 82 0.154339 -0.118181 0.20070 0.983 1.98e-02 0.01501
## 83 -0.032130 0.013088 -0.08038 1.018 3.24e-03 0.01007
## 84 0.095684 -0.085264 0.10046 1.051 5.08e-03 0.03506
## 85 0.070968 -0.058086 0.08335 1.033 3.50e-03 0.01906
## 86 0.035724 -0.017750 0.07759 1.019 3.02e-03 0.01035
## 87 0.043186 -0.038113 0.04582 1.052 1.06e-03 0.03181
## 88 0.029005 -0.021268 0.04028 1.032 8.18e-04 0.01359
## 89 0.045105 -0.025154 0.08818 1.016 3.90e-03 0.01067
## 90 0.225683 -0.182605 0.26969 0.961 3.53e-02 0.01810
## 91 0.226986 -0.198448 0.24351 1.010 2.94e-02 0.02919
## 92 0.224470 -0.198589 0.23752 1.020 2.80e-02 0.03258
## 93 -0.017647 0.014745 -0.02011 1.042 2.04e-04 0.02121
## 94 0.109797 -0.088129 0.13282 1.018 8.82e-03 0.01752
## 95 -0.047652 0.040510 -0.05300 1.042 1.42e-03 0.02358
## 96 -0.036866 0.068902 0.14021 1.003 9.78e-03 0.01293
## 97 0.164822 -0.130238 0.20421 0.987 2.05e-02 0.01653
## 98 0.091397 -0.077440 0.10212 1.035 5.24e-03 0.02307
## 99 -0.092328 0.076526 -0.10645 1.030 5.69e-03 0.02029
## 100 -0.096939 0.077518 -0.11793 1.022 6.97e-03 0.01726
## 101 -0.003765 0.002012 -0.00767 1.031 2.97e-05 0.01053
## 102 0.001089 -0.000855 0.00136 1.037 9.38e-07 0.01617
# Question 4:
# Calculate muitple linear regression for prestige score ~ education + income + women.
n <- lm(Prestige_Score ~ Education + Income + Percent_of_Women, data = occupation.prestige) ; n
##
## Call:
## lm(formula = Prestige_Score ~ Education + Income + Percent_of_Women,
## data = occupation.prestige)
##
## Coefficients:
## (Intercept) Education Income Percent_of_Women
## -6.794334 4.186637 0.001314 -0.008905
# Display summary of n.
summary(n)
##
## Call:
## lm(formula = Prestige_Score ~ Education + Income + Percent_of_Women,
## data = occupation.prestige)
##
## Residuals:
## Min 1Q Median 3Q Max
## -19.8246 -5.3332 -0.1364 5.1587 17.5045
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -6.7943342 3.2390886 -2.098 0.0385 *
## Education 4.1866373 0.3887013 10.771 < 2e-16 ***
## Income 0.0013136 0.0002778 4.729 7.58e-06 ***
## Percent_of_Women -0.0089052 0.0304071 -0.293 0.7702
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.846 on 98 degrees of freedom
## Multiple R-squared: 0.7982, Adjusted R-squared: 0.792
## F-statistic: 129.2 on 3 and 98 DF, p-value: < 2.2e-16
# Display ANOVA table of n.
anova(n)
## Analysis of Variance Table
##
## Response: Prestige_Score
## Df Sum Sq Mean Sq F value Pr(>F)
## Education 1 21608.4 21608.4 350.9741 < 2.2e-16 ***
## Income 1 2248.1 2248.1 36.5153 2.739e-08 ***
## Percent_of_Women 1 5.3 5.3 0.0858 0.7702
## Residuals 98 6033.6 61.6
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Calculate the F-statistic for df = 3, 98 and alpha = 0.025.
qf(0.975, df1 = 3, df2 = 98)
## [1] 3.252415
# Question 5.
# Calculate t-statistic to test with.
qt(0.0975, df = 98)
## [1] -1.304849
# Determine confidence intervals for regression variables.
confint(n, conf.level = 0.95)
## 2.5 % 97.5 %
## (Intercept) -1.322220e+01 -0.366468202
## Education 3.415272e+00 4.958002277
## Income 7.623127e-04 0.001864808
## Percent_of_Women -6.924697e-02 0.051436660
# Generate residual plots with fitted values against residuals.
par(mfrow = c(1,2))
plot(fitted(n), resid(n), axes = TRUE, frame.plot = TRUE,
col = "steelblue", pch = 20, ann = FALSE)
abline(h = 0, lty = 2)
title(main = "Residuals vs. Fitted (Without Curve)", xlab = "Fitted values", ylab = "Residuals")
mtext("Residuals vs Fitted", side = 3, line = 0.25)
plot(n, which = 1, col = "steelblue", pch = 20, ann = TRUE)
title(main = "Residuals vs. Fitted (With Curve)")
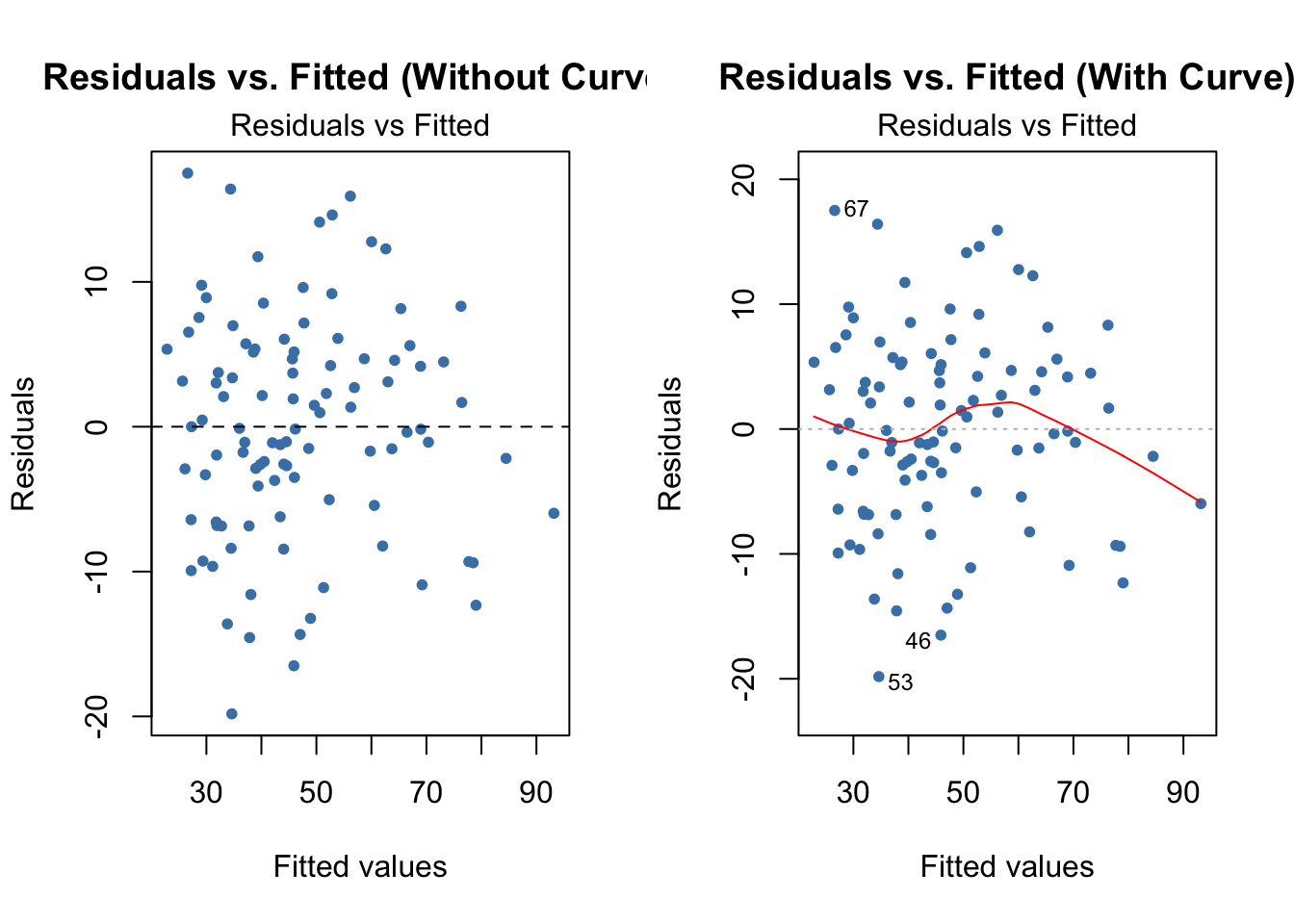
# Determine influential points.
influence.measures(n)
## Influence measures of
## lm(formula = Prestige_Score ~ Education + Income + Percent_of_Women, data = occupation.prestige) :
##
## dfb.1_ dfb.Edct dfb.Incm dfb.P__W dffit cov.r cook.d
## 1 -2.31e-02 8.73e-03 4.60e-02 -2.87e-03 9.82e-02 1.056 2.43e-03
## 2 -1.04e-01 6.21e-01 -1.04e+00 -4.87e-01 -1.07e+00 1.448 2.83e-01
## 3 -2.45e-02 3.87e-02 -6.39e-03 -2.65e-02 8.04e-02 1.045 1.63e-03
## 4 6.08e-03 9.59e-03 2.89e-03 -2.65e-02 6.56e-02 1.045 1.08e-03
## 5 -1.25e-01 1.99e-01 -1.22e-01 -1.27e-01 2.35e-01 1.043 1.38e-02
## 6 -8.44e-02 1.09e-01 -4.10e-02 -6.59e-02 1.39e-01 1.086 4.88e-03
## 7 -1.02e-01 1.39e-01 -7.57e-02 -5.66e-02 1.59e-01 1.068 6.39e-03
## 8 -2.64e-02 2.25e-02 9.79e-03 -1.12e-02 4.98e-02 1.094 6.27e-04
## 9 -5.24e-02 6.87e-02 -1.53e-02 -5.20e-02 1.09e-01 1.071 2.97e-03
## 10 2.26e-03 -3.11e-03 9.96e-04 2.34e-03 -4.55e-03 1.087 5.23e-06
## 11 -4.66e-02 1.82e-01 -1.82e-01 -1.95e-01 2.55e-01 1.027 1.62e-02
## 12 -2.44e-02 8.48e-02 -7.24e-02 -8.76e-02 1.29e-01 1.043 4.17e-03
## 13 9.21e-02 -1.49e-01 8.32e-02 9.25e-02 -1.91e-01 1.026 9.07e-03
## 14 2.39e-02 -2.12e-02 3.06e-03 -1.13e-02 -3.73e-02 1.078 3.52e-04
## 15 -1.91e-01 2.16e-01 -9.12e-02 1.60e-02 2.97e-01 0.970 2.17e-02
## 16 8.44e-02 -1.00e-01 5.31e-02 -1.15e-02 -1.37e-01 1.060 4.74e-03
## 17 3.33e-02 2.70e-03 -6.74e-02 -1.79e-02 -9.68e-02 1.152 2.36e-03
## 18 2.72e-02 -2.36e-02 6.58e-03 -2.23e-02 -4.86e-02 1.091 5.95e-04
## 19 2.00e-01 -2.11e-01 5.46e-02 2.20e-02 -2.83e-01 0.997 1.99e-02
## 20 -2.29e-01 5.10e-01 -4.70e-01 -4.04e-01 5.85e-01 1.027 8.39e-02
## 21 -1.67e-01 1.55e-01 5.41e-03 -3.42e-02 2.44e-01 1.043 1.48e-02
## 22 -3.76e-02 2.82e-02 -4.62e-03 4.57e-02 7.92e-02 1.089 1.58e-03
## 23 7.06e-03 -7.75e-03 3.04e-03 -8.56e-05 -1.00e-02 1.086 2.55e-05
## 24 8.99e-02 1.54e-01 -4.41e-01 -2.01e-01 -4.96e-01 1.335 6.17e-02
## 25 2.28e-01 -1.90e-01 -7.51e-02 7.74e-02 -3.96e-01 0.990 3.86e-02
## 26 9.77e-02 2.84e-02 -2.52e-01 -6.58e-02 -3.53e-01 1.058 3.10e-02
## 27 -1.30e-01 4.85e-02 3.35e-02 3.44e-01 4.61e-01 0.958 5.19e-02
## 28 -1.12e-02 1.48e-02 -7.62e-03 -3.30e-02 -4.41e-02 1.078 4.91e-04
## 29 -2.31e-01 2.03e-01 -7.61e-02 2.41e-01 4.77e-01 0.914 5.50e-02
## 30 1.84e-02 -2.00e-02 4.31e-03 5.20e-03 -2.74e-02 1.082 1.89e-04
## 31 -1.43e-01 1.21e-01 -3.76e-02 2.06e-01 3.73e-01 0.931 3.39e-02
## 32 1.15e-02 5.62e-02 -6.36e-02 -6.32e-02 1.43e-01 0.992 5.10e-03
## 33 -7.86e-03 1.92e-02 -1.39e-02 -1.67e-02 2.77e-02 1.067 1.94e-04
## 34 2.26e-03 1.06e-02 -6.18e-03 -1.97e-02 3.67e-02 1.054 3.39e-04
## 35 7.96e-04 1.42e-04 -6.35e-04 -4.14e-03 -5.21e-03 1.105 6.85e-06
## 36 1.31e-02 -4.45e-03 8.85e-04 -6.06e-02 -8.40e-02 1.096 1.78e-03
## 37 -8.83e-03 1.04e-02 -8.27e-03 4.28e-02 7.68e-02 1.059 1.49e-03
## 38 -1.69e-03 -1.72e-03 -2.39e-03 4.45e-02 6.34e-02 1.092 1.01e-03
## 39 -5.45e-03 2.82e-03 -4.35e-04 2.96e-02 4.48e-02 1.073 5.07e-04
## 40 -7.00e-02 -4.47e-04 5.30e-02 6.83e-02 -1.24e-01 1.029 3.82e-03
## 41 1.11e-01 -1.29e-01 1.09e-01 -1.99e-01 -4.03e-01 0.942 3.96e-02
## 42 9.66e-03 -5.64e-04 1.58e-03 -7.95e-02 -1.11e-01 1.086 3.09e-03
## 43 -3.02e-02 3.23e-03 1.61e-02 2.86e-02 -5.10e-02 1.056 6.56e-04
## 44 -1.03e-02 -3.46e-04 1.12e-02 -1.39e-02 -4.40e-02 1.055 4.89e-04
## 45 -4.50e-04 1.19e-02 -1.01e-02 -6.13e-02 -7.61e-02 1.099 1.46e-03
## 46 1.59e-02 -9.09e-02 1.03e-01 -3.82e-02 -2.70e-01 0.877 1.76e-02
## 47 -3.45e-03 1.05e-02 -8.95e-03 4.04e-02 8.78e-02 1.041 1.94e-03
## 48 1.30e-02 -5.19e-02 3.29e-02 -2.33e-02 -1.87e-01 0.936 8.54e-03
## 49 6.78e-03 -2.28e-02 3.03e-02 -7.79e-02 -1.64e-01 1.015 6.70e-03
## 50 -2.12e-02 1.35e-02 -9.01e-03 4.26e-03 -3.76e-02 1.051 3.57e-04
## 51 -3.37e-02 -2.21e-02 2.16e-03 9.75e-02 -1.87e-01 0.974 8.67e-03
## 52 -3.47e-02 -2.09e-03 5.76e-02 -1.19e-01 -2.52e-01 0.976 1.56e-02
## 53 -1.25e-01 -3.40e-01 6.15e-01 5.10e-01 -7.08e-01 0.834 1.18e-01
## 54 -8.00e-02 -2.15e-01 3.71e-01 3.42e-01 -4.51e-01 0.945 4.95e-02
## 55 -4.06e-05 -2.43e-02 1.15e-02 3.40e-02 -7.62e-02 1.039 1.46e-03
## 56 -2.32e-03 -3.93e-03 2.93e-03 4.06e-03 -1.97e-02 1.051 9.76e-05
## 57 3.57e-03 -8.87e-04 3.73e-03 -3.82e-04 1.95e-02 1.051 9.58e-05
## 58 -1.19e-02 8.67e-03 -6.85e-03 5.61e-03 -2.01e-02 1.065 1.02e-04
## 59 3.98e-03 6.56e-04 7.14e-04 -8.35e-03 1.65e-02 1.060 6.86e-05
## 60 7.05e-03 -5.94e-03 1.33e-03 4.63e-03 1.01e-02 1.072 2.59e-05
## 61 -1.79e-01 3.54e-02 1.03e-01 1.14e-01 -2.60e-01 0.937 1.66e-02
## 62 3.71e-02 4.20e-03 -7.91e-03 -5.85e-02 1.14e-01 1.022 3.23e-03
## 63 -2.80e-02 2.65e-02 2.14e-02 -1.49e-01 -2.25e-01 1.071 1.27e-02
## 64 -1.11e-01 1.25e-01 -6.09e-02 -1.29e-01 -1.89e-01 1.064 8.93e-03
## 65 -1.93e-01 1.41e-01 -1.83e-02 -3.47e-02 -2.19e-01 1.002 1.19e-02
## 66 -1.58e-01 9.88e-02 6.93e-03 -6.37e-03 -1.85e-01 1.006 8.50e-03
## 67 3.91e-01 -1.78e-01 -9.20e-02 -1.90e-01 4.53e-01 0.871 4.90e-02
## 68 -1.05e-01 -2.42e-02 1.44e-01 8.31e-02 -2.15e-01 1.006 1.15e-02
## 69 -5.42e-02 2.39e-02 7.25e-04 3.79e-02 -7.87e-02 1.053 1.56e-03
## 70 1.56e-01 -1.21e-01 2.89e-02 3.66e-02 1.82e-01 1.012 8.28e-03
## 71 -1.18e-01 8.07e-02 -1.56e-02 1.16e-02 -1.32e-01 1.036 4.39e-03
## 72 5.42e-02 -3.69e-02 7.12e-03 -5.32e-03 6.05e-02 1.061 9.23e-04
## 73 -4.64e-02 4.63e-02 -1.37e-02 -5.30e-02 -8.33e-02 1.086 1.75e-03
## 74 1.45e-01 -1.28e-01 4.95e-02 4.06e-02 1.62e-01 1.049 6.54e-03
## 75 6.64e-02 -5.65e-02 1.67e-02 2.39e-02 7.68e-02 1.072 1.49e-03
## 76 -2.73e-02 7.17e-03 -1.56e-03 3.02e-02 -6.00e-02 1.052 9.06e-04
## 77 7.16e-02 -3.58e-02 3.15e-03 -3.95e-02 9.88e-02 1.043 2.45e-03
## 78 -1.66e-02 9.17e-03 -1.32e-03 8.13e-03 -2.13e-02 1.066 1.15e-04
## 79 1.24e-01 -8.39e-02 2.64e-02 -3.52e-02 1.47e-01 1.035 5.39e-03
## 80 -1.60e-03 9.31e-04 -1.07e-04 4.38e-04 -1.96e-03 1.062 9.74e-07
## 81 6.89e-02 -3.52e-02 3.29e-03 -3.52e-02 9.36e-02 1.044 2.20e-03
## 82 1.71e-01 -2.36e-01 1.52e-01 3.55e-01 4.53e-01 0.898 4.93e-02
## 83 -3.29e-02 -4.36e-02 7.45e-02 9.68e-02 -1.28e-01 1.041 4.14e-03
## 84 1.21e-01 -1.69e-01 1.10e-01 1.89e-01 2.36e-01 1.131 1.40e-02
## 85 5.59e-02 -2.62e-02 -4.90e-03 -3.23e-02 7.10e-02 1.061 1.27e-03
## 86 3.55e-02 -3.83e-03 -6.12e-03 -4.64e-02 8.13e-02 1.045 1.67e-03
## 87 2.30e-05 -1.33e-05 -5.25e-07 -8.92e-06 2.55e-05 1.084 1.64e-10
## 88 -1.46e-02 1.06e-02 -6.82e-03 5.67e-03 -2.17e-02 1.065 1.18e-04
## 89 4.90e-02 -1.18e-03 -1.89e-02 -6.57e-02 1.07e-01 1.036 2.87e-03
## 90 2.11e-01 -1.97e-01 1.45e-01 -2.05e-02 2.86e-01 0.980 2.02e-02
## 91 2.20e-01 -1.37e-01 1.32e-02 -7.70e-02 2.45e-01 1.011 1.49e-02
## 92 1.86e-01 -1.38e-01 4.43e-02 -3.91e-02 2.03e-01 1.044 1.03e-02
## 93 -3.38e-02 1.20e-02 1.07e-02 2.22e-02 -4.34e-02 1.070 4.75e-04
## 94 9.20e-02 -5.59e-02 1.55e-02 -4.16e-02 1.18e-01 1.045 3.49e-03
## 95 -6.12e-02 1.90e-02 2.52e-02 4.31e-02 -7.95e-02 1.070 1.59e-03
## 96 1.53e-03 -2.03e-02 5.76e-02 2.88e-03 8.33e-02 1.080 1.75e-03
## 97 1.41e-01 -1.26e-01 9.20e-02 -2.44e-02 1.97e-01 1.022 9.64e-03
## 98 7.02e-02 -4.59e-02 8.60e-03 -1.64e-02 7.91e-02 1.060 1.57e-03
## 99 -1.12e-01 3.13e-02 4.90e-02 8.19e-02 -1.51e-01 1.039 5.75e-03
## 100 -1.23e-01 2.19e-02 6.49e-02 1.15e-01 -1.85e-01 1.021 8.50e-03
## 101 -8.60e-03 4.37e-04 3.52e-03 8.10e-03 -1.83e-02 1.055 8.46e-05
## 102 2.31e-02 -2.81e-02 1.52e-02 3.93e-02 5.34e-02 1.080 7.19e-04
## hat inf
## 1 0.0270
## 2 0.3422 *
## 3 0.0176
## 4 0.0145
## 5 0.0464
## 6 0.0538
## 7 0.0457
## 8 0.0498
## 9 0.0389
## 10 0.0414
## 11 0.0433
## 12 0.0262
## 13 0.0309
## 14 0.0348
## 15 0.0331
## 16 0.0367
## 17 0.0988 *
## 18 0.0467
## 19 0.0380
## 20 0.1021
## 21 0.0479
## 22 0.0485
## 23 0.0407
## 24 0.2435 *
## 25 0.0558
## 26 0.0753
## 27 0.0569
## 28 0.0359
## 29 0.0484
## 30 0.0379
## 31 0.0363
## 32 0.0132
## 33 0.0249
## 34 0.0154
## 35 0.0572
## 36 0.0542
## 37 0.0254
## 38 0.0489
## 39 0.0317
## 40 0.0193
## 41 0.0434
## 42 0.0500
## 43 0.0188
## 44 0.0171
## 45 0.0556
## 46 0.0154 *
## 47 0.0173
## 48 0.0117
## 49 0.0221
## 50 0.0129
## 51 0.0167
## 52 0.0271
## 53 0.0646 *
## 54 0.0517
## 55 0.0138
## 56 0.0104
## 57 0.0106
## 58 0.0223
## 59 0.0173
## 60 0.0285
## 61 0.0211
## 62 0.0151
## 63 0.0588
## 64 0.0484
## 65 0.0280
## 66 0.0232
## 67 0.0366 *
## 68 0.0287
## 69 0.0219
## 70 0.0245
## 71 0.0238
## 72 0.0238
## 73 0.0463
## 74 0.0352
## 75 0.0345
## 76 0.0176
## 77 0.0201
## 78 0.0233
## 79 0.0259
## 80 0.0188
## 81 0.0196
## 82 0.0415
## 83 0.0251
## 84 0.0978 *
## 85 0.0260
## 86 0.0180
## 87 0.0385
## 88 0.0227
## 89 0.0187
## 90 0.0337
## 91 0.0358
## 92 0.0409
## 93 0.0288
## 94 0.0250
## 95 0.0334
## 96 0.0412
## 97 0.0306
## 98 0.0263
## 99 0.0287
## 100 0.0281
## 101 0.0132
## 102 0.0379
