# Install and load libraries.
library(xlsx)
## Loading required package: rJava
## Loading required package: xlsxjars
library(plyr)
# Import data from 'homework5data.xlsx' using xlsx function.
iq.data <- read.xlsx("homework5data.xlsx", sheetName = "Sheet1", header = TRUE)
# View summary of iq.data.
summary(iq.data)
## group iq age
## Chemistry student:15 Min. :20.00 Min. :14.00
## Maths student :15 1st Qu.:36.00 1st Qu.:17.00
## Physics student :15 Median :40.00 Median :18.00
## Mean :39.96 Mean :26.13
## 3rd Qu.:46.00 3rd Qu.:40.00
## Max. :52.00 Max. :58.00
#----------
# Question 1.
#----------
# Determine the number of students in each group.
table(iq.data$group)
##
## Chemistry student Maths student Physics student
## 15 15 15
# Determine if 'group' is a factor; if 'true', proceed ; otherwise, create factor.
is.factor(iq.data$group)
## [1] TRUE
# Summarize data relating to IQ score by group of students.
ddply(iq.data, "group", summarise,
N = length(iq),
mean = mean(iq),
sd = sd(iq))
## group N mean sd
## 1 Chemistry student 15 48.20000 2.396426
## 2 Maths student 15 35.86667 6.937133
## 3 Physics student 15 35.80000 7.793770
# Summarize data relating to age by group of students.
ddply(iq.data, "group", summarise,
N = length(age),
mean = mean(age),
sd = sd(age))
## group N mean sd
## 1 Chemistry student 15 44.33333 6.651172
## 2 Maths student 15 17.33333 1.046536
## 3 Physics student 15 16.73333 1.437591
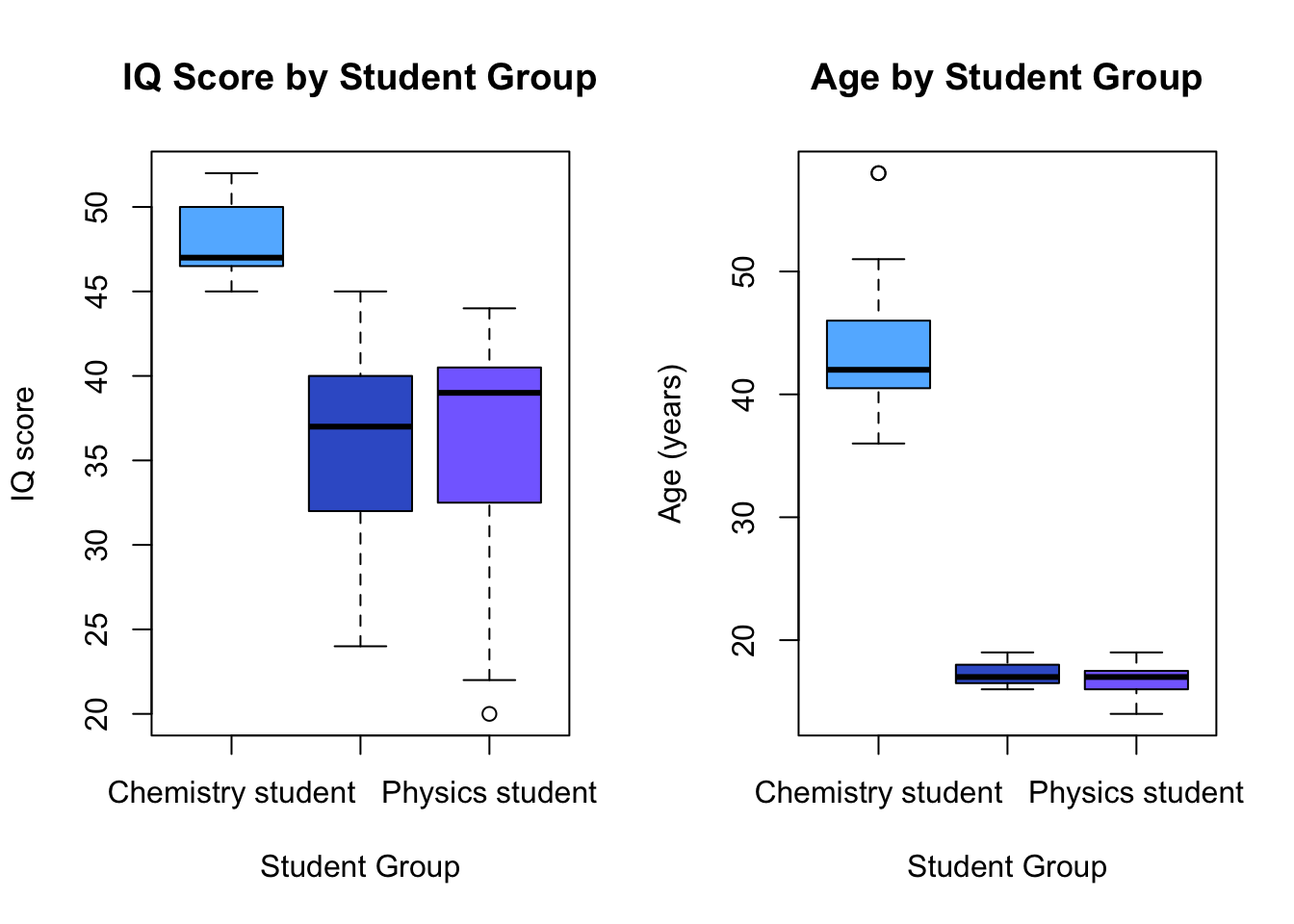
# Generate boxplots for each group.
par(mfrow = c(1, 2)) # Set par settings for two side-by-side plots
boxplot(iq.data$iq ~ iq.data$group, data = iq.data,
main = "IQ Score by Student Group", ylab = "IQ score",
xlab = "Student Group",
col = c("steelblue1", "royalblue3", "lightslateblue"))
boxplot(iq.data$age ~ iq.data$group, data = iq.data,
main = "Age by Student Group", ylab = "Age (years)",
xlab = "Student Group",
col = c("steelblue1", "royalblue3", "lightslateblue"))
par(mfrow = c(1, 1)) # Reset par settings
#----------
# Question 2.
#----------
# Calculate F-statistic to compare against.
qf(0.95, df1 = 2, df2 = 12)
## [1] 3.885294
# Perform a one-way ANOVA for IQ scores.
m <- aov(iq.data$iq ~ iq.data$group) ; m
## Call:
## aov(formula = iq.data$iq ~ iq.data$group)
##
## Terms:
## iq.data$group Residuals
## Sum of Squares 1529.378 1604.533
## Deg. of Freedom 2 42
##
## Residual standard error: 6.180872
## Estimated effects may be unbalanced
summary(m)
## Df Sum Sq Mean Sq F value Pr(>F)
## iq.data$group 2 1529 764.7 20.02 7.84e-07 ***
## Residuals 42 1604 38.2
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
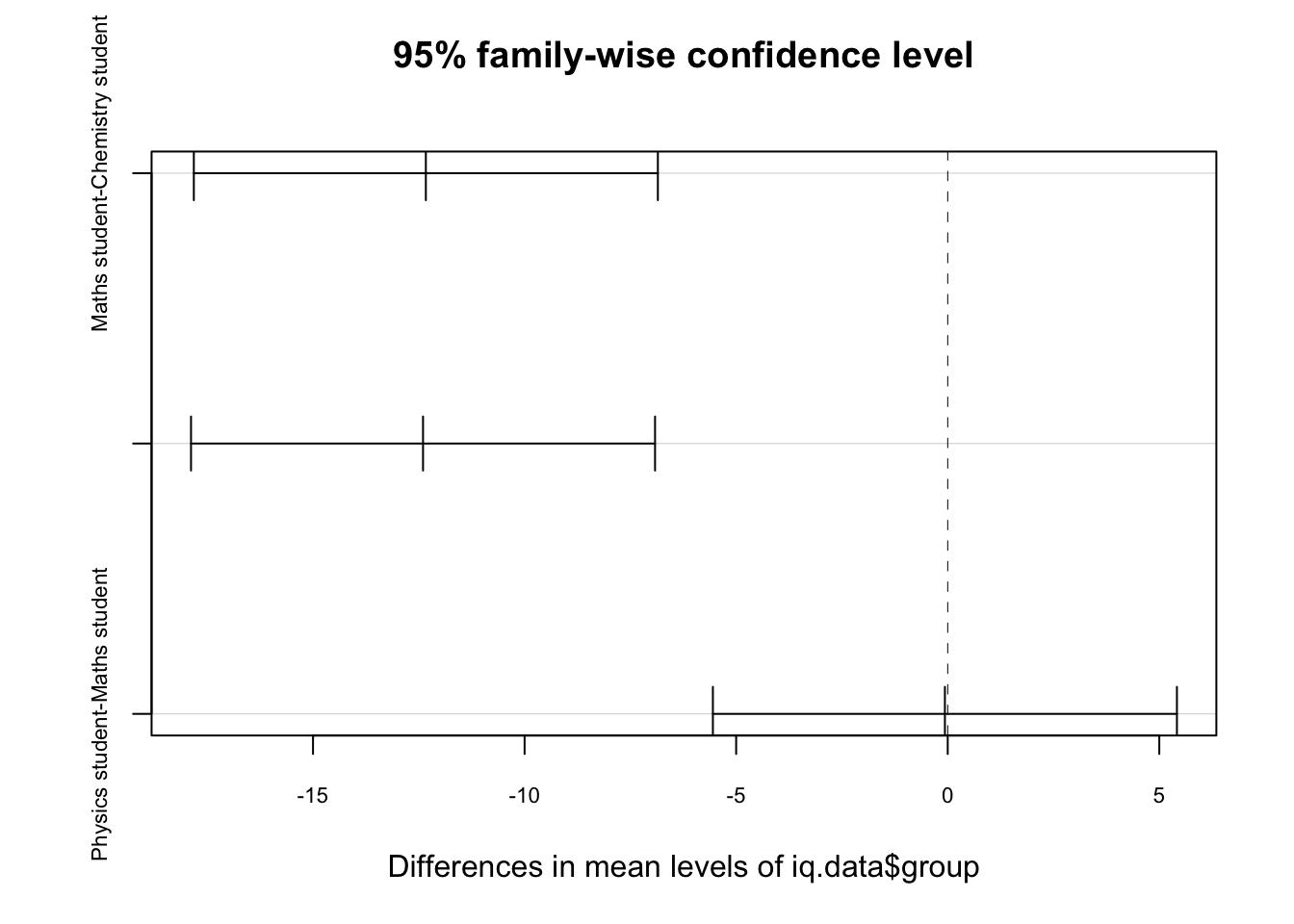
# Perform Tukey's procedure. Display mean diff. conf. intervals.
TukeyHSD(m)
## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = iq.data$iq ~ iq.data$group)
##
## $`iq.data$group`
## diff lwr upr
## Maths student-Chemistry student -12.33333333 -17.816543 -6.850123
## Physics student-Chemistry student -12.40000000 -17.883210 -6.916790
## Physics student-Maths student -0.06666667 -5.549877 5.416543
## p adj
## Maths student-Chemistry student 0.0000069
## Physics student-Chemistry student 0.0000062
## Physics student-Maths student 0.9995191
plot(TukeyHSD(m), cex.axis = 0.7)
#----------
# Question 3
#----------
# Create dummy variables for student group (chemistry is reference).
iq.data$g.maths <- ifelse(iq.data$group == "Maths student", 1, 0)
iq.data$g.maths
## [1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0
## [36] 0 0 0 0 0 0 0 0 0 0
iq.data$g.phys <- ifelse(iq.data$group == "Physics student", 1, 0)
iq.data$g.phys
## [1] 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [36] 0 0 0 0 0 0 0 0 0 0
head(iq.data) ; tail(iq.data)
## group iq age g.maths g.phys
## 1 Physics student 44 15 0 1
## 2 Physics student 40 17 0 1
## 3 Physics student 44 15 0 1
## 4 Physics student 39 14 0 1
## 5 Physics student 25 19 0 1
## 6 Physics student 37 18 0 1
## group iq age g.maths g.phys
## 40 Chemistry student 47 44 0 0
## 41 Chemistry student 46 46 0 0
## 42 Chemistry student 45 38 0 0
## 43 Chemistry student 50 58 0 0
## 44 Chemistry student 47 41 0 0
## 45 Chemistry student 49 42 0 0
# Perform one-way ANOVA test using lm function (including dummies).
m2 <- lm(iq.data$iq ~ iq.data$g.maths + iq.data$g.phys)
summary(m2)
##
## Call:
## lm(formula = iq.data$iq ~ iq.data$g.maths + iq.data$g.phys)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.800 -2.200 1.133 3.800 9.133
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 48.200 1.596 30.203 < 2e-16 ***
## iq.data$g.maths -12.333 2.257 -5.465 2.33e-06 ***
## iq.data$g.phys -12.400 2.257 -5.494 2.11e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 6.181 on 42 degrees of freedom
## Multiple R-squared: 0.488, Adjusted R-squared: 0.4636
## F-statistic: 20.02 on 2 and 42 DF, p-value: 7.843e-07
#----------
# Question 4
#----------
# Re-run ANOVA adjusting for age using Anova function.
require(car)
## Loading required package: car
## Warning: package 'car' was built under R version 3.4.4
## Loading required package: carData
## Warning: package 'carData' was built under R version 3.4.4
options(contrasts = c("contr.treatment", "contr.poly"))
Anova(lm(iq.data$iq ~ iq.data$group + iq.data$age), type = 3)
## Anova Table (Type III tests)
##
## Response: iq.data$iq
## Sum Sq Df F value Pr(>F)
## (Intercept) 740.02 1 18.9123 8.842e-05 ***
## iq.data$group 114.82 2 1.4672 0.2424
## iq.data$age 0.25 1 0.0064 0.9367
## Residuals 1604.28 41
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
# Generate Least Squares means.
require(lsmeans)
## Loading required package: lsmeans
## The 'lsmeans' package is being deprecated.
## Users are encouraged to switch to 'emmeans'.
## See help('transition') for more information, including how
## to convert 'lsmeans' objects and scripts to work with 'emmeans'.
options(contrasts = c("contr.treatment", "contr.poly"))
lsmeans(lm(iq.data$iq ~ iq.data$group + iq.data$age),
pairwise ~ iq.data$group, adjust = "none")
## $lsmeans
## iq.data$group lsmean SE df lower.CL upper.CL
## Chemistry student 35.76639 1.669056 41 32.39567 39.13712
## Maths student 35.80517 1.616411 41 32.54076 39.06958
## Physics student 35.76639 1.669056 41 32.39567 39.13712
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio
## Chemistry student - Maths student -0.03877838 0.4856523 41 -0.08
## Chemistry student - Physics student 0.00000000 0.0000000 41 NaN
## Maths student - Physics student 0.03877838 0.4856523 41 0.08
## p.value
## 0.9367
## NaN
## 0.9367

